Lecture 11
Molecular Clocks and Tree Space
1. Understanding Tree Space
Before diving into molecular clocks, we need to understand the mathematical space in which phylogenetic trees exist. This "tree space" has unique geometric properties that affect how we search for optimal trees and summarize posterior distributions.
Tree Space for Time Trees
Consider the simplest non-trivial case: time trees for 3 taxa.
A two-dimensional space representing all possible time-trees for the topology ((1,2),3). The axes x and y are the two inter-coalescent intervals, with $t_{root} = x + y$
Tree Subspace Properties
- Each tree topology defines a subspace
- For time trees with $n$ taxa, each subspace is $(n-1)$-dimensional
- The dimensions can be parameterized as:
- Inter-coalescent intervals: Forms a hypercube (all intervals independent)
- Node heights: Forms a simplex (heights must respect temporal ordering)
- Trees can be averaged within a subspace (arithmetic mean shown)
- Distances between trees can be computed (Euclidean distance shown as dashed lines)
The Complete Tree Space
The complete tree space for 3 taxa showing how topology subspaces connect
Key features of tree space:
- Each non-degenerate tree topology is a two-dimensional space
- These subspaces meet at shared edges representing degenerate topologies
- The star tree (all three taxa diverge simultaneously) is a one-dimensional subspace
- The parameter for the star tree is just the age of the root
Key insight: Tree space has both discrete (topology) and continuous (branch lengths/node times) components. MCMC must explore both!
Alternative Visualizations of Tree Space
Tree space using node height parameterization, where temporal constraints create simplices (triangular regions) rather than hypercubes
Parameterization matters: When using node heights as parameters, the constraint that parent nodes must be older than child nodes creates simplices. In contrast, inter-coalescent intervals are independent, creating hypercubes.
Higher-Dimensional Tree Spaces
For 4 taxa, the tree space becomes more complex:
Projection of 4-taxa tree space. The full space has 18 subspaces (only 6 shown). Each subspace is actually a 3D cube, shown as squares by fixing one dimension
Tree Space Complexity
As the number of taxa increases:
- 3 taxa: 3 ranked topologies, 2D subspaces
- 4 taxa: 18 ranked topologies, 3D subspaces
- 5 taxa: 180 ranked topologies, 4D subspaces
For 4 taxa: There are 15 rooted topologies total. Of these:
- 12 are "caterpillar" trees (fully pectinate) - each has only 1 ranking
- 3 are balanced trees - each has 2 possible rankings of the two internal nodes on the same side of the root
- Total: 12 × 1 + 3 × 2 = 18 ranked topologies
Note: Each subspace corresponds to a ranked topology where the temporal order of all coalescence events is specified. When parameterized by inter-coalescent intervals, each subspace forms a hypercube (all intervals can vary independently). When parameterized by node heights, the subspaces form simplices due to temporal ordering constraints.
Implications for Phylogenetic Inference
Understanding tree space helps us appreciate:
- Complexity of the search problem: Tree space grows super-exponentially with taxa
- Need for specialized moves: MCMC operators must handle both discrete topology changes and continuous parameter updates
- Challenges in summarization: Averaging trees across topologies is problematic
- Local optima: The discrete nature creates barriers between topology subspaces
2. The Molecular Clock Hypothesis
Genetic Distance = Rate × Time
The fundamental equation of molecular evolution:
The Molecular Clock Equation
$$d = \mu \times t$$
Where:
- $d$ = genetic distance (expected substitutions per site)
- $\mu$ = substitution rate (substitutions per site per unit time)
- $t$ = time
The Strict Molecular Clock
Under a strict molecular clock, all lineages evolve at the same rate:
The strict clock: a single rate $\mu$ converts the time tree to a substitution tree
Strict Molecular Clock
- Single evolutionary rate $\mu$ for all branches
- Ultrametric trees (all tips equidistant from root)
- Proposed by Zuckerkandl and Pauling (1962)
- Enables dating without fossils if rate is known
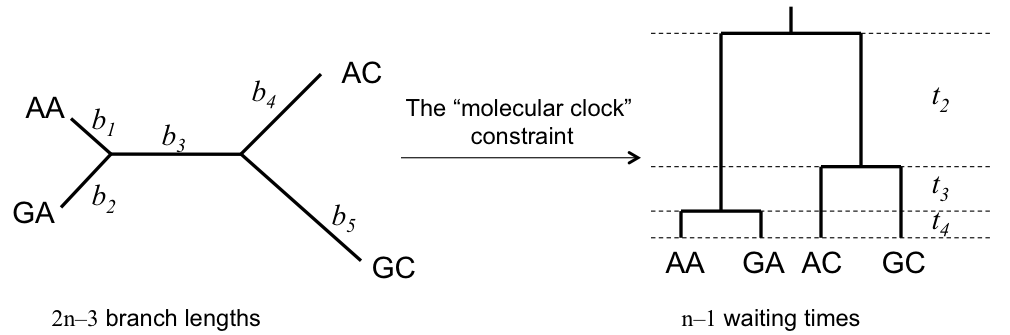
3. The Identifiability Problem
Non-identifiability of Rate and Time
Without calibration, infinitely many combinations of rate and time produce the same genetic distances
Fundamental problem: From genetic distances alone, we cannot separate rate from time. If we double all times and halve the rate, we get the same likelihood!
Solutions to the Identifiability Problem
To separate rate and time, we need additional information:
1. Node Calibrations
Use fossil or biogeographic evidence to constrain node ages:
Fossil evidence constraining the age of the ABC ancestor to 25-35 Mya
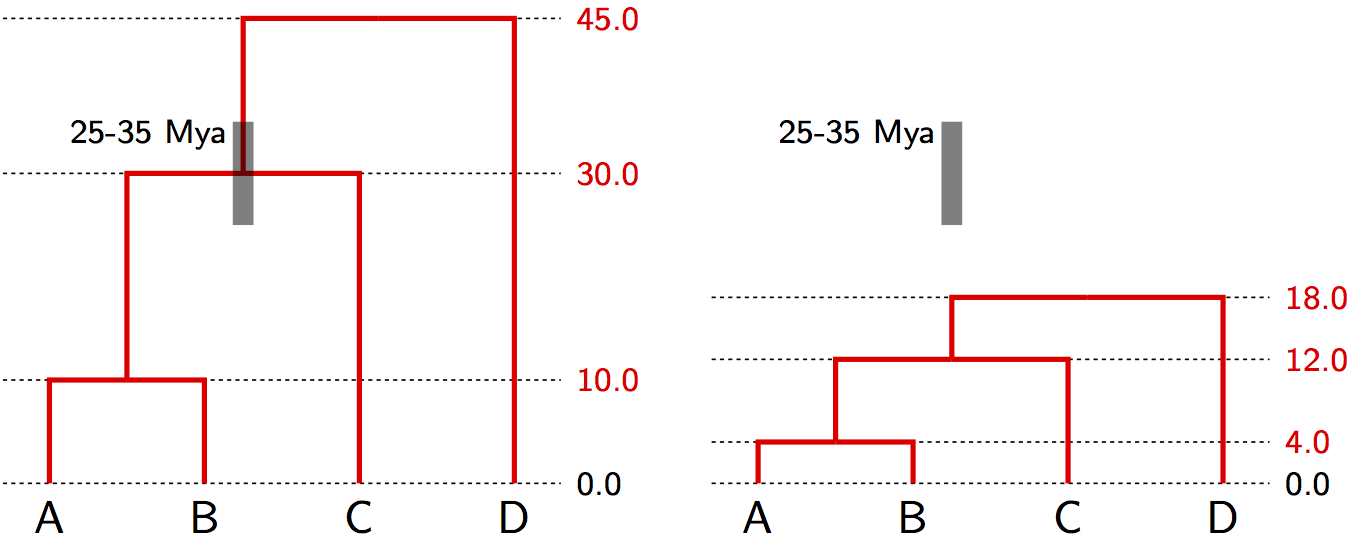
Node Calibration in Practice
- Fossil provides minimum age (fossil must be younger than clade)
- Biogeography can provide maximum age (e.g., island age)
- Often specified as probability distributions (e.g., lognormal)
- Multiple calibrations improve precision
2. Tip Calibrations
Use samples from different time points:
Ancient DNA from sample C (20,000 years old) provides temporal information
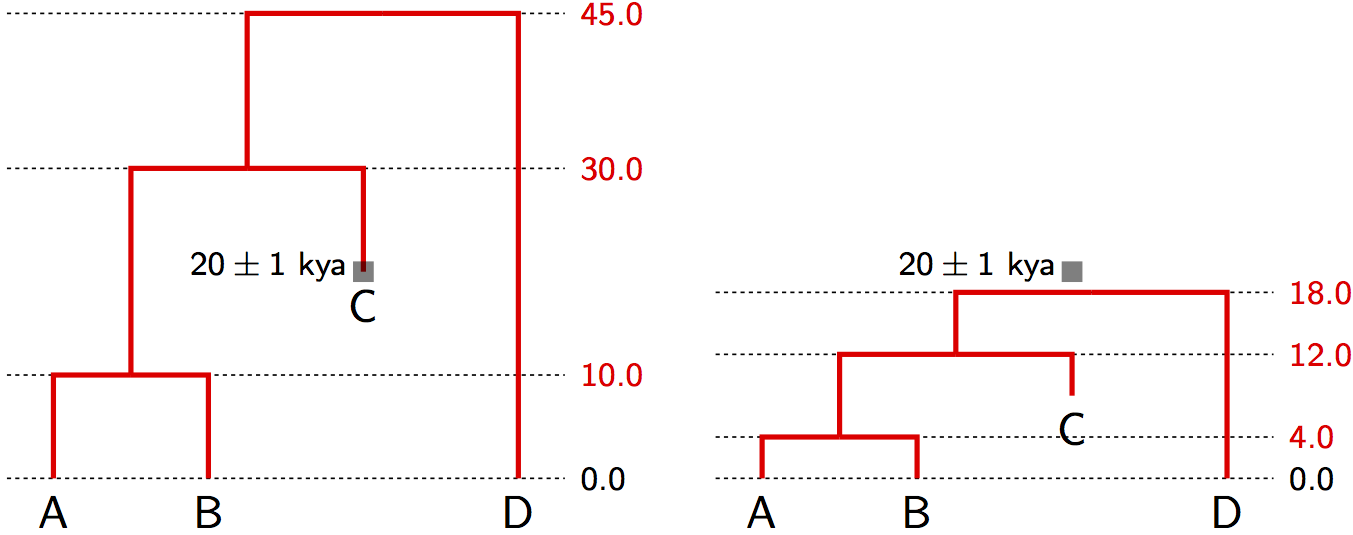
Applications of Tip Calibration
- Ancient DNA: Subfossil remains, museum specimens
- Rapidly evolving pathogens: Virus samples from different years
- Laboratory evolution: Samples from known time points
Key principle: With either node or tip calibration, knowing even one absolute time allows us to estimate all other times under a strict clock.
4. Relaxed Molecular Clocks
The strict molecular clock is often too restrictive. Relaxed clocks allow rate variation across branches.
Relaxed Clock Parameterization
Each branch has its own rate, converting time tree to substitution tree
Relaxed Molecular Clock
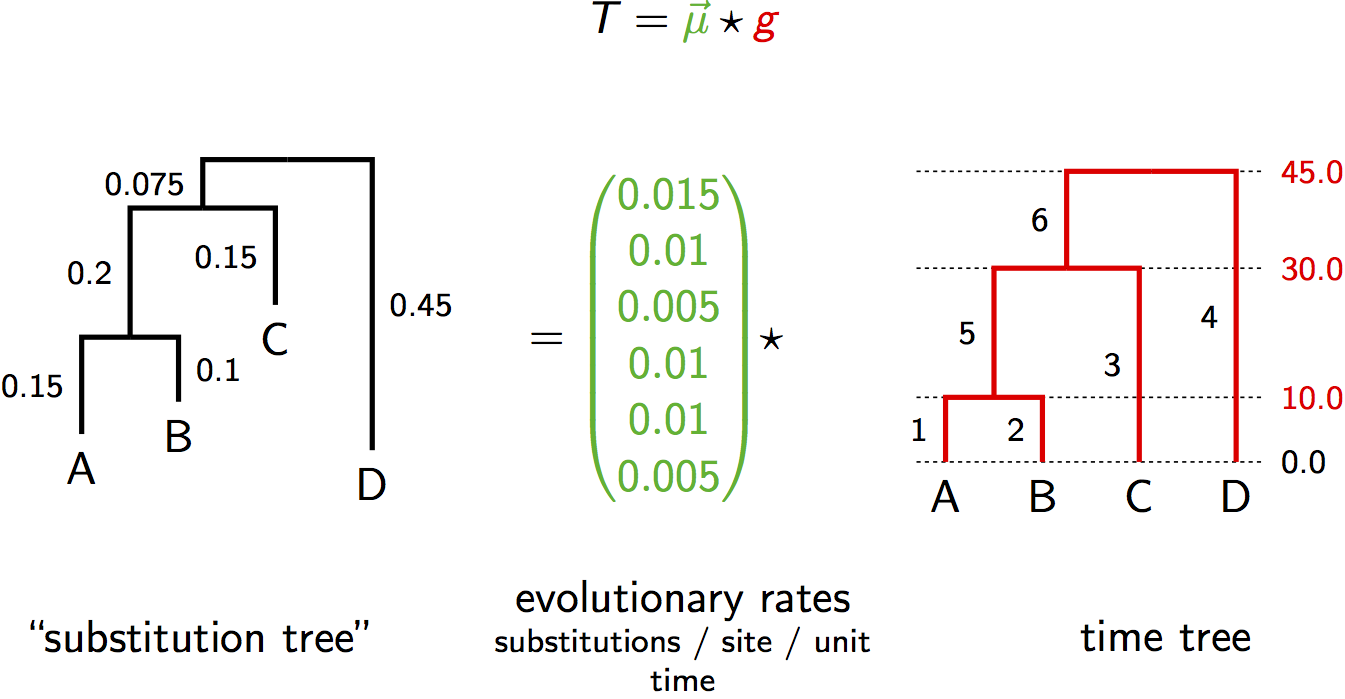
Instead of a single rate $\mu$, we have a vector of rates $\vec{\mu} = (\mu_1, \mu_2, ..., \mu_{2n-2})$
The substitution tree is computed as: $T = \vec{\mu} \star g$
Where $\star$ denotes element-wise multiplication of rates and branch durations
Alternative Relaxed Clock Visualization
Another view showing how branch-specific rates create the substitution tree
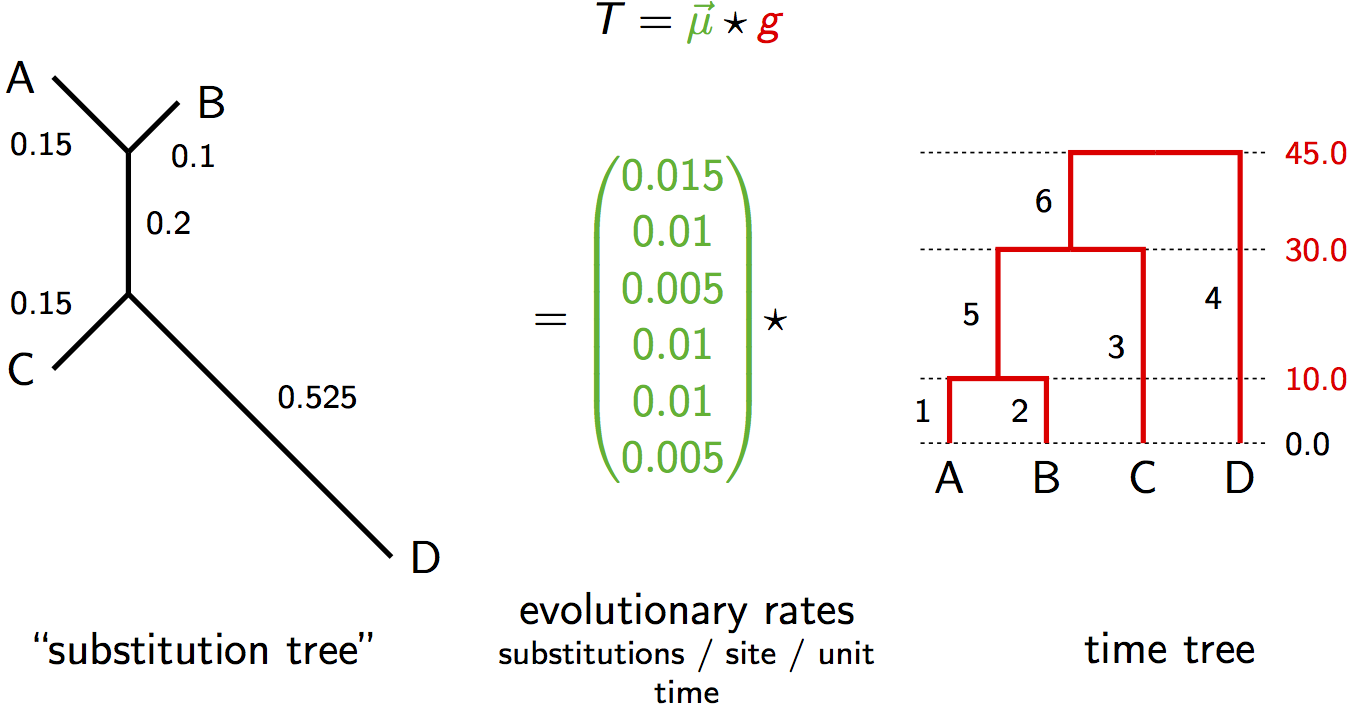
Identifiability Under Relaxed Clocks
With relaxed clocks, the identifiability problem is even more severe
Critical issue: Relaxed clocks are only identifiable through their priors! The likelihood alone cannot distinguish between fast rates with short times vs. slow rates with long times.
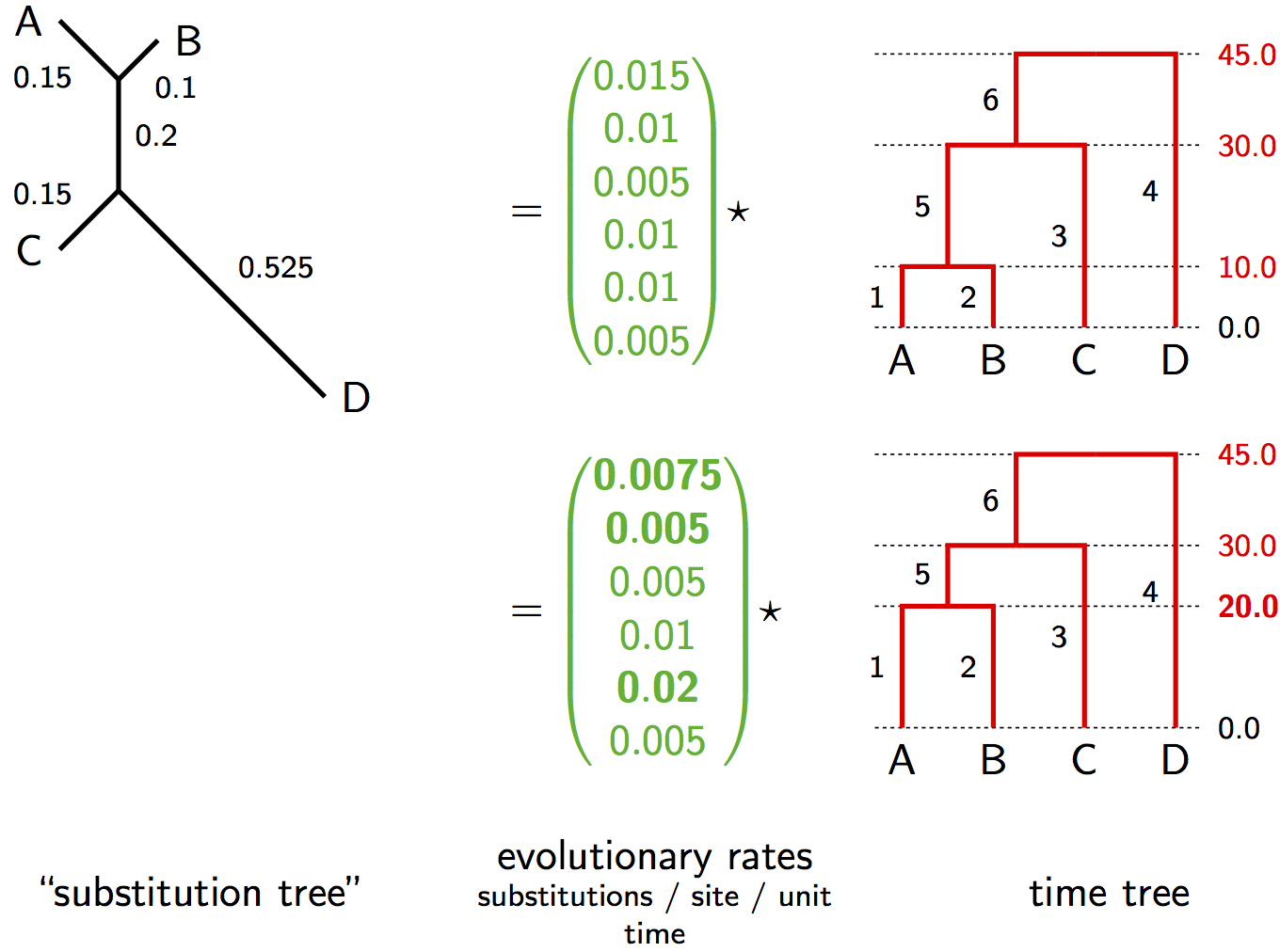
5. Bayesian Framework for Molecular Clocks
Posterior with Strict Clock
Strict Clock Posterior
Substitution tree: $T = \textcolor{darkgreen}{\mu} \times \textcolor{red}{g}$
$$P(\textcolor{red}{g}, \textcolor{darkgreen}{\mu}, \theta|D) = \frac{1}{\Pr(D)}\Pr(D|T)P(\textcolor{red}{g}|\theta)P(\textcolor{darkgreen}{\mu})P(\theta)$$
Where:
- $\textcolor{red}{g}$ = time tree
- $\textcolor{darkgreen}{\mu}$ = clock rate
- $\theta$ = other model parameters
Posterior with Relaxed Clock
Relaxed Clock Posterior
Substitution tree: $T = \textcolor{darkgreen}{\vec{\mu}} \star \textcolor{red}{g}$
$$P(\textcolor{red}{g}, \textcolor{darkgreen}{\vec{\mu}},\theta|D) = \frac{1}{\Pr(D)}\Pr(D|T)P(\textcolor{red}{g}|\theta)P(\textcolor{darkgreen}{\vec{\mu}})P(\theta)$$
Where $P(\textcolor{darkgreen}{\vec{\mu}})$ is the prior for rate variation
Key observations:
- The phylogenetic likelihood only depends on the substitution tree $T$: $\Pr(D|T)$
- The tree prior only depends on the time tree $\textcolor{red}{g}$: $P(\textcolor{red}{g}|\theta)$
- By fixing $\textcolor{darkgreen}{\vec{\mu}} = 1$, we get a time tree in units of substitutions
6. Models of Rate Variation
Autocorrelated Models
Rates evolve along the tree, with child rates similar to parent rates:
Autocorrelated Rate Model
$$P(\textcolor{darkgreen}{\vec{\mu}}) = \prod_i P(\mu_i | \mu_{\text{parent}(i)})$$
Common implementation: Lognormal autocorrelated model
$$\log(\mu_i) \sim \text{Normal}(\log(\mu_{\text{parent}(i)}), \sigma \sqrt{t_i})$$
Where:
- $t_i$ = time duration of branch $i$
- $\sigma$ = rate of evolution of rates (volatility parameter)
Uncorrelated Models
Rates are drawn independently for each branch:
Uncorrelated Rate Model
$$P(\textcolor{darkgreen}{\vec{\mu}}) = \prod_i P(\mu_i | \nu)$$
Common implementations:
- Lognormal: $\log(\mu_i) \sim \text{Normal}(M, S)$
- Exponential: $\mu_i \sim \text{Exponential}(\lambda)$
- Gamma: $\mu_i \sim \text{Gamma}(\alpha, \beta)$
Autocorrelated
- Biologically motivated
- Smooth rate changes
- Good for closely related species
- Can extrapolate rates
Uncorrelated
- More flexible
- Allows sudden rate changes
- Good for diverse datasets
- Simpler to implement
7. Parameter Dimensions
Understanding the number of parameters helps us appreciate model complexity:
Unrooted Tree (No Clock)
- $2n-3$ branch lengths (one per branch)
- Total: $2n-3$ parameters
Strict Molecular Clock
- $n-1$ node heights (internal nodes)
- 1 clock rate $\mu$
- Total: $n$ parameters
Relaxed Molecular Clock
- $n-1$ node heights
- $2n-2$ rate parameters (one per branch)
- Total: $3n-3$ parameters
Overparameterization: Relaxed clocks have more parameters than unrooted trees! They are only identifiable through their priors.
8. MCMC Implementation Differences
MrBayes Approach (No Clock)
MrBayes samples unrooted trees without molecular clock constraints:
- Operators must connect any unrooted tree to any other
- Branch lengths can be any positive value
- No temporal constraints
- Simpler operators but no time information
BEAST Approach (With Clock)
BEAST samples rooted time trees with clock constraints:
- Operators must maintain temporal constraints
- All tips fixed at their sampling times
- Internal nodes must be older than descendants
- Natural to work with node heights rather than branch lengths
MCMC operators must respect the constraint that parent nodes are older than children
Clock-Constrained Operators
Examples of operators that maintain temporal constraints:
- Scale: Multiply all node heights by a factor
- Subtree slide: Move subtree up/down while maintaining order
- Wilson-Balding: Prune and regraft with valid node times
- Uniform node height: Sample new height within valid bounds
9. Advantages of Molecular Clock Models
Relaxed molecular clocks offer several benefits over unconstrained models:
- Improved phylogenetic accuracy:
- Rate smoothing helps identify correct topology
- Reduces long-branch attraction artifacts
- Better performance on empirical datasets
- Automatic rooting:
- No need for outgroup
- Root position estimated from rate variation
- Particularly useful when outgroup is distant
- Temporal information:
- Relative divergence times always available
- Absolute times with calibration
- Useful for studying evolutionary rates
- Integration with other models:
- Natural combination with coalescent priors
- Enables epidemiological inference
- Links to fossil data
Best practice: Use relaxed clocks unless you have strong evidence for a strict clock. The added flexibility usually outweighs the increased parameter count.
Summary
This lecture covered two interrelated topics crucial for modern phylogenetics:
- Tree space geometry:
- Trees exist in a complex space with discrete and continuous components
- Each topology defines a subspace of dimension $n-1$
- Understanding tree space helps design better algorithms
- Molecular clocks:
- Fundamental equation: distance = rate × time
- Rate and time are non-identifiable without calibration
- Strict clocks assume constant rates
- Relaxed clocks allow rate variation
- Bayesian implementation:
- Priors essential for identifiability
- Different parameterizations for different software
- MCMC must respect temporal constraints
- Practical advantages:
- Better tree estimation
- Automatic rooting
- Temporal information
- Integration with other evolutionary models
Key takeaway: Molecular clocks transform phylogenetics from estimating relationships to understanding the tempo and mode of evolution.
Recommended Reading:
- Drummond & Bouckaert (2015) "Bayesian Evolutionary Analysis with BEAST" - Chapters 6-7
- Yang (2014) "Molecular Evolution: A Statistical Approach" - Chapter 7
- Drummond et al. (2006) "Relaxed phylogenetics and dating with confidence" - PLOS Biology
- Billera et al. (2001) "Geometry of the space of phylogenetic trees" - Advances in Applied Mathematics
Check Your Understanding
- Why is tree space not a simple Euclidean space?
- What makes rate and time non-identifiable in molecular evolution?
- How do node and tip calibrations solve the identifiability problem?
- What's the key difference between autocorrelated and uncorrelated relaxed clocks?
- Why do relaxed clocks often produce better phylogenetic estimates than no-clock models?