Lecture 9
MCMC in Phylogenetics
1. The Phylogenetic Likelihood
At the heart of Bayesian phylogenetic inference is the phylogenetic likelihood:
$$P(D|T, \mu)$$
Where:
- $D$ is a multiple sequence alignment of $n$ sequences
- $T$ is a phylogenetic tree with $n$ leaves
- $\mu$ are the parameters of the chosen CTMC-based model of sequence evolution
Computing the Likelihood
The phylogenetic likelihood is computed using Felsenstein's pruning algorithm (covered in Lecture 7). Key points:
- The likelihood is a product of site pattern probabilities
- Sites are assumed to evolve independently
- This assumption allows for obvious generalizations:
- Multiple alignments that share a tree
- Phylogenetic networks where different sites evolve under distinct "local" trees
Key insight: As Bayesians, we need a probability distribution for $T$! The likelihood alone is not sufficient.
2. The Phylogenetic Posterior
Standard application of Bayes' theorem gives the posterior:
$$P(T,\mu,\theta|D) = \frac{P(D|T,\mu, \theta)P(T,\mu,\theta)}{P(D)}$$
Factorizing the Posterior
Most phylogenetic models make two key assumptions:
- $\theta$ only affects the probability of the data via the tree $T$
- $\mu$ has no effect on the tree branching process
These assumptions lead to the factorized form:
Phylogenetic Posterior
$$P(T,\mu,\theta|D) = \frac{1}{P(D)}P(D|T,\mu)P(T|\theta)P(\mu,\theta)$$
Where:
- $P(T|\theta)$ is the "tree prior" parameterized by $\theta$
- $P(\mu,\theta)$ are the parameter priors
- $P(D)$ is the marginal likelihood (evidence)
Questions to Consider
- What is $P(D)$ and why is it difficult to compute?
- Is the tree prior really a prior? (i.e., does it depend on the data?)
The Neutrality Assumption
The factorization above implicitly assumes that our alignment could have been produced through the following process:
Three-step process: (1) Generate tree from branching process, (2) Evolve sequences along branches, (3) Observe sequences at tips
Important: Separating the process of tree generation from that of sequence evolution implies neutrality. This is a fundamental assumption in most phylogenetic analyses.
3. Tree Priors
Tree priors allow us to specify a generative model for the genealogy. While this model may not involve genetic evolution, it may depend on:
- Speciation rates
- Population sizes
- Migration rates
- Extinction rates
- Sampling processes
Note: A huge fraction of phylogenetics inference research is focused on developing and efficiently implementing tree priors!
The Yule Model for Speciation
The simplest tree prior is the Yule model (Yule, 1924):
Yule Process
- Constant rate branching process
- Branching occurs uniformly across extant lineages at rate $\lambda$ per lineage per unit time
- Chemical kinetics formalism: $X \overset{\lambda}{\longrightarrow} 2X$
The number of lineages $k$ evolves under the master equation:
$$\dot{p}(k,t) = \lambda (k-1)p(k-1,t) - \lambda k p(k,t)$$
Example of a tree generated under the Yule process
Birth-Death(-Sampling) Priors
A more realistic model accounts for both speciation and extinction:
Birth-Death Process
- Generalization of Yule process to account for extinction and sampling
- Linear speciation, extinction, and sampling rates
- Prior is over sampled trees: assumes unobserved full tree
- Groundwork largely due to Tanja Stadler (ETH Zürich)
Birth-death tree showing sampled (solid) and unsampled (dashed) lineages
Coalescent Priors
For modeling gene trees within populations:
Coalescent Process
- Original theory due to Kingman (1980)
- Models the shape of gene trees within a species
- Can be obtained as the limit of population genetic models (Wright-Fisher, Moran)
- Provides crucial link between tree shape and population size
Relationship between tree shape and effective population size under the coalescent
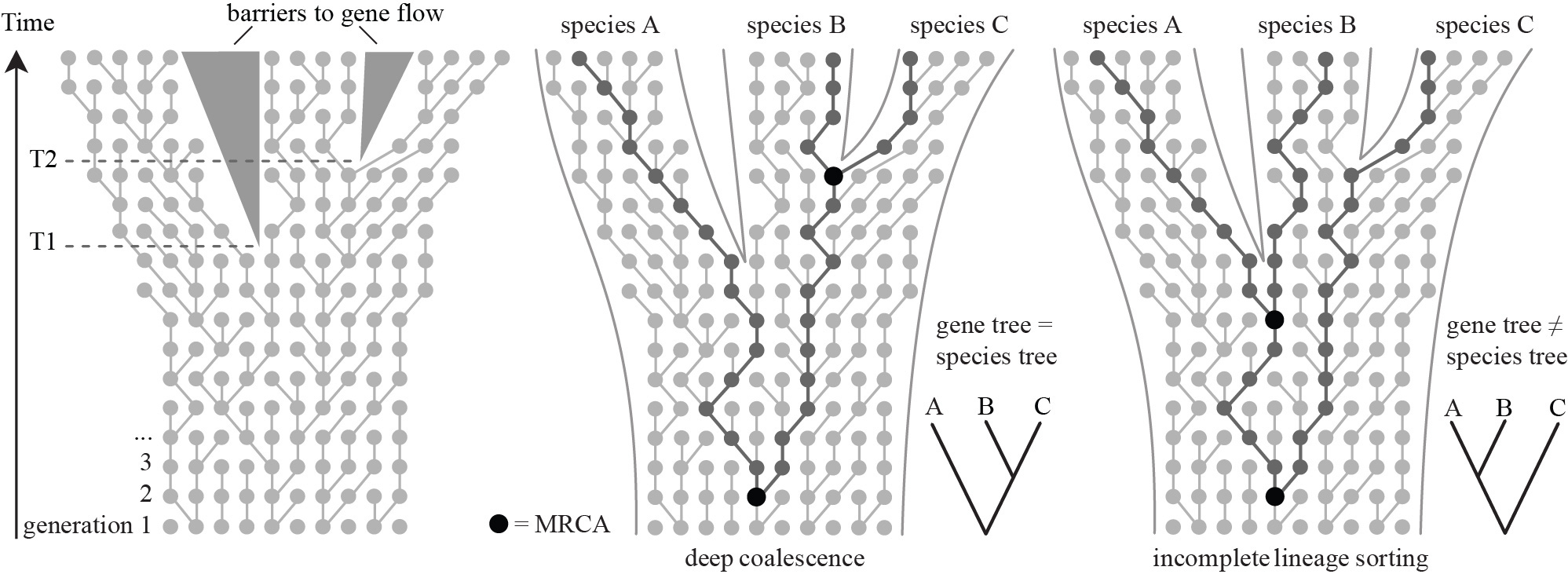
Multi-species Coalescent Priors
Hierarchical models that embed gene trees within species trees:
- Species tree described using a birth-death prior
- Gene trees described by coalescent priors for populations which subdivide at speciation events
- Accounts for incomplete lineage sorting
Gene trees (thin lines) embedded within a species tree (thick lines)
4. MCMC in Tree Space
Basic MCMC Theory Review
MCMC works by simulating a stochastic trajectory according to:
$$p_{i+1}(x)=\int p_i(x')W(x|x')\mathrm{d}x'$$
Where the transition kernel is:
$$W(x'|x) = q(x'|x)\alpha(x'|x) + \left(1-\int q(x''|x)\alpha(x''|x)\mathrm{d}x''\right)\delta(x'-x)$$
Detailed Balance and Acceptance Probability
A sufficient condition for $\pi(x)$ to be the equilibrium distribution is detailed balance:
$$\pi(x')q(x|x')\alpha(x|x')=\pi(x)q(x'|x)\alpha(x'|x)$$
This is satisfied by the Metropolis-Hastings acceptance probability:
Metropolis-Hastings Acceptance
$$\alpha(x'|x)=\min\left[1, \frac{\pi(x')}{\pi(x)}\times\frac{q(x|x')}{q(x'|x)}\right]$$
Key Properties for Tree Space
- By tuning the acceptance probability, any probability distribution can be targeted
- Only the ratio $\pi(x')/\pi(x)$ appears: normalization need not be known
- The only requirement for $q(x'|x)$ is irreducibility: random walks must explore the entire state space
- For high-dimensional state spaces, $W(x'|x)$ is decomposed into several distinct operators: $W(x'|x)=\sum_j W_j(x'|x)$
- The ratio $q(x|x')/q(x'|x)$ is the Hastings ratio
5. Proposal Distributions for Trees
We need to identify a set of proposals $q_j(x'|x)$ when $x$ is a point in the space of rooted time trees.
Common tree operators: (A) Subtree slide, (B) Wilson-Balding, (C) Exchange, (D) Scale
Common Tree Operators
- Subtree Slide
- Move a subtree up or down along a branch, changing node heights
- Wilson-Balding
- Prune a subtree and regraft it elsewhere, sampling new node times
- Narrow/Wide Exchange
- Swap two subtrees that share a grandparent (narrow) or any two subtrees (wide)
- Node Height Changes
- Modify the height of internal nodes while maintaining time consistency
- Tree Scaling
- Scale all node heights by a common factor
Challenge: Each operator must maintain the constraint that parent nodes are older than their children (time consistency).
Hastings Ratios for Tree Operators
Computing the Hastings ratio for tree operators can be complex:
- Must account for changes in the number of possible attachment points
- Node height proposals may have different forward/reverse probabilities
- Some operators (e.g., uniform tree scaling) have trivial Hastings ratios
Example: Subtree Slide Hastings Ratio
For a subtree slide that moves node $v$ from time $t$ to $t'$:
- If heights are proposed uniformly in valid ranges
- Forward range: $(t_{\text{child}}, t_{\text{parent}})$
- Reverse range: $(t'_{\text{child}}, t'_{\text{parent}})$
- Hastings ratio: $\frac{t'_{\text{parent}} - t'_{\text{child}}}{t_{\text{parent}} - t_{\text{child}}}$
6. Convergence and Mixing
Stopping Criteria
Two critical questions for phylogenetic MCMC:
- How can we tell when the chain has reached equilibrium?
- How do we know when we've collected enough samples?
Effective Sample Size (ESS)
One approach is to compute ESS for each parameter and tree summary statistics:
- ESS estimates the number of independent samples
- Common statistics to monitor:
- Tree height (age of root)
- Tree length (sum of branch lengths)
- Model parameters (substitution rates, etc.)
- Rule of thumb: ESS > 200 for all parameters
Multiple Independent Runs
Best Practice: Always run multiple independent chains with different starting points. Convergence to the same distribution is necessary (but not sufficient) for equilibrium.
Assessing Tree Convergence
Trees present special challenges for convergence assessment:
- Cannot plot simple traces of "the tree"
- Need specialized statistics for tree space
- Common approaches:
- Compare split frequencies between runs
- Average standard deviation of split frequencies (ASDSF)
- Tree distance metrics between samples
AWTY (Are We There Yet?)
Software that applies multiple statistics to assess tree convergence:
AWTY/RWTY visualization of convergence diagnostics across multiple runs
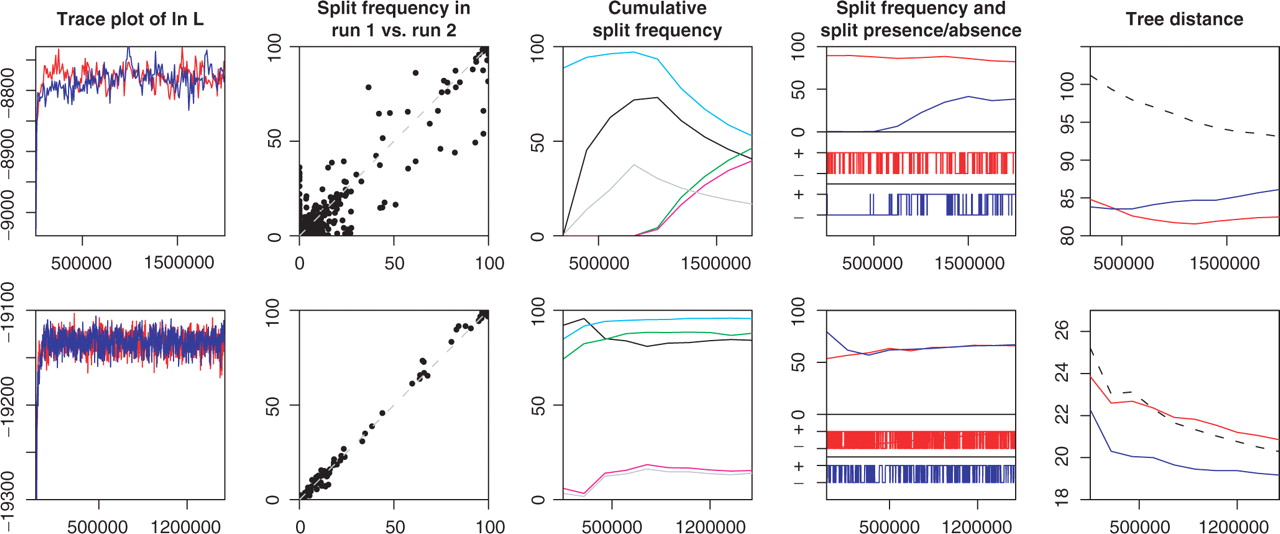
Key diagnostics:
- Split frequency correlations between runs
- Cumulative split frequencies over time
- Tree space visualization using multidimensional scaling
7. Post-processing MCMC Output
Parameter Samples
Logs of individual parameters can be considered samples from marginal posteriors:
Tracer software showing parameter traces and marginal distributions
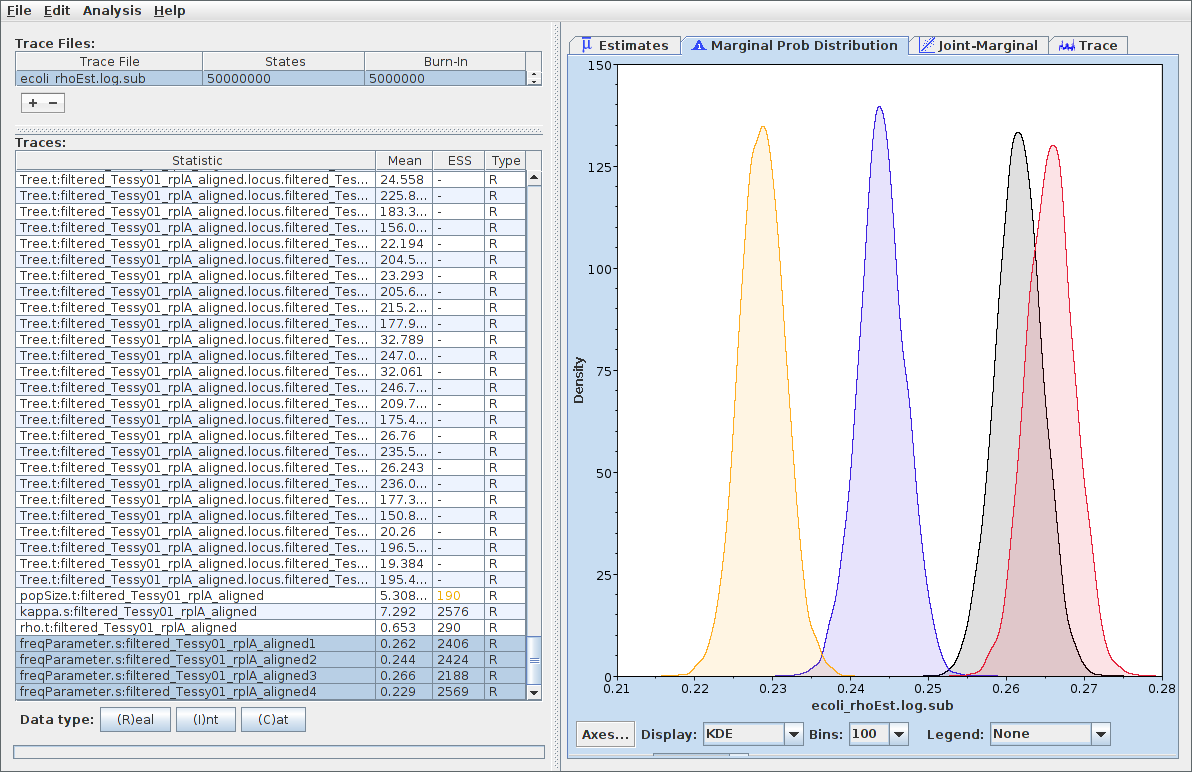
Common analyses:
- Marginal density estimation
- 95% credible intervals
- Mean/median estimates
- Correlation between parameters
Tree Samples
Summary Statistics
Extract specific information from sampled trees:
- Age of MRCA for clades of interest
- Posterior probabilities of clades
- Branch length distributions
- Tree balance statistics
Summary Trees
Different approaches to produce a single "summary" tree:
- Strict Consensus
- Include only clades that appear in ALL sampled trees
- Majority Rule Consensus
- Include clades that appear in >50% of sampled trees
- Maximum Clade Credibility (MCC) Tree
- The sampled topology for which the product of posterior clade probabilities is maximized
In BEAST: Summary trees are produced using the MCC tree method via the program TreeAnnotator.
Caution: No summary tree algorithm is perfect! They may be misleading when the posterior is multimodal. Consider reporting uncertainty using posterior probabilities.
8. Bayesian Phylogenetic Software
General Purpose Software
- MrBayes (Huelsenbeck and Ronquist, 2001)
-
- Early command-line program for phylogenetic inference
- Implements standard substitution models and tree priors
- Widely used and well-tested
- RevBayes (Höhna et al., 2016)
-
- R-like syntax for specifying phylogenetic models
- Highly flexible model specification
- Growing ecosystem of tutorials and methods
- BEAST/BEAST 2 (Drummond and Rambaut, 2007; Bouckaert et al., 2014)
-
- XML specification of phylogenetic models
- Extensible through packages
- Strong focus on time-calibrated trees
- Integrated with other tools (BEAUti, Tracer, TreeAnnotator)
Specialized Software
- MIGRATE
- Performs inference under the Structured Coalescent (subpopulation sizes, migration rates, ancestral locations)
- ClonalFrame/ClonalOrigin
- Infer bacterial Ancestral Recombination Graphs (generalizations of trees when recombination is present)
Software Ecosystem
- BEAUti: GUI for creating BEAST XML files
- Tracer: MCMC trace analysis and diagnostics
- FigTree: Tree visualization and annotation
- DensiTree: Visualizing sets of trees
- SPREAD: Spatial phylogenetic reconstruction
Summary
This lecture covered the practical aspects of Bayesian phylogenetic inference using MCMC:
- Phylogenetic posterior: Combines tree likelihood with tree priors under neutrality assumption
- Tree priors:
- Yule process (pure birth)
- Birth-death-sampling models
- Coalescent and multi-species coalescent
- MCMC in tree space:
- Requires specialized operators
- Must maintain time consistency
- Complex Hastings ratios
- Convergence assessment:
- ESS for parameters and tree statistics
- Multiple independent runs essential
- Specialized diagnostics for trees
- Post-processing:
- Parameter estimation straightforward
- Tree summarization challenging
- Report uncertainty, not just point estimates
Key takeaways:
- Tree priors link tree shape to biological processes
- MCMC makes Bayesian phylogenetics computationally feasible
- Convergence assessment is crucial but challenging
- No single summary can capture complex posteriors
Recommended Reading:
- Felsenstein (2004) "Inferring Phylogenies" - Chapters 26-27
- Drummond & Bouckaert (2015) "Bayesian Evolutionary Analysis with BEAST" - Chapters 4-5
- Yang (2014) "Molecular Evolution: A Statistical Approach" - Chapter 7
- Höhna et al. (2016) "RevBayes: Bayesian phylogenetic inference" - Systematic Biology
Check Your Understanding
- Why does the phylogenetic posterior factorization imply neutral evolution?
- What's the difference between birth-death and coalescent tree priors?
- Why do we need specialized operators for tree space MCMC?
- What makes ESS a useful but imperfect convergence diagnostic?
- Why might an MCC tree be misleading for multimodal posteriors?