Maximum Parsimony - Bayesian phylogenetics lectures

1. Characters and Character States

To understand parsimony, we first need to understand the fundamental units of phylogenetic analysis: characters and character states.

Key Definitions

Character: A feature that can vary among organisms (e.g., a nucleotide position in DNA, presence/absence of wings)
Character state: The specific condition of a character in a particular organism (e.g., A, C, G, or T at a DNA position)
Character matrix: A table showing character states for all taxa across all characters

Example character matrix for DNA sequences:

Taxon	Character (position)
	1	2	3	4	5	6	7	8	9	10
Human	A	G	C	T	A	C	G	G	T	A
Chimp	A	G	C	T	A	C	G	A	T	A
Gorilla	A	G	T	T	G	C	G	A	T	C
Orangutan	A	A	T	C	G	T	A	A	C	C

Similarities and differences in character states provide evidence for inferring evolutionary relationships.

When Do Characters Support the Correct Tree?

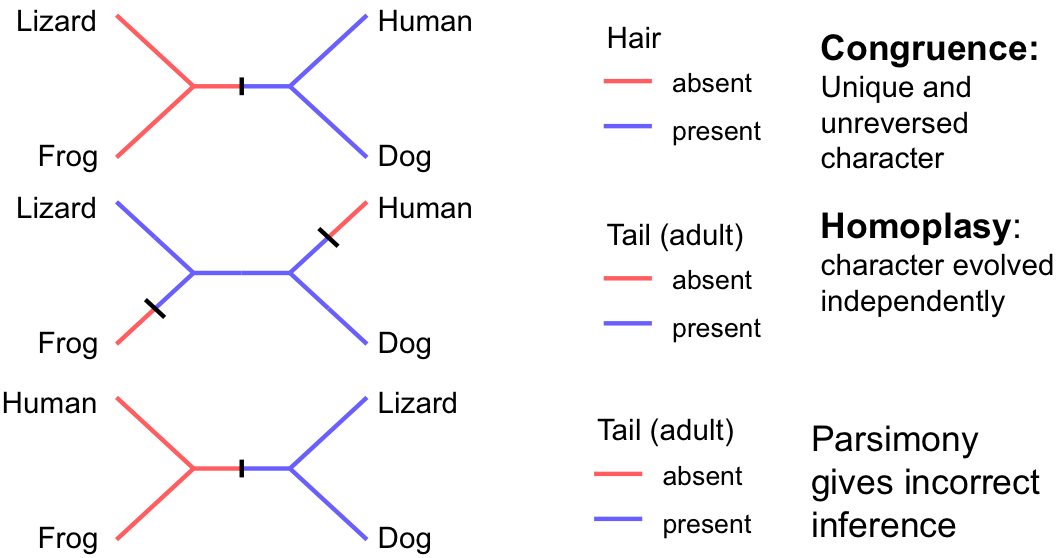
Characters supporting phylogenetic trees

Characters provide evidence for phylogenetic relationships through shared derived states

Characters support correct phylogenetic inference when:

Shared character states reflect common ancestry (homology)
Changes are rare enough that multiple changes to the same state are uncommon
There's sufficient variation to be informative

The Problem of Homoplasy

Homoplasy

Similarity in character states that is not due to common ancestry. This can arise from:

Convergent evolution: Independent evolution of similar traits
Parallel evolution: Independent evolution along similar pathways
Reversals: Return to an ancestral character state

Reversals

Reversals to ancestral states can mislead phylogenetic inference

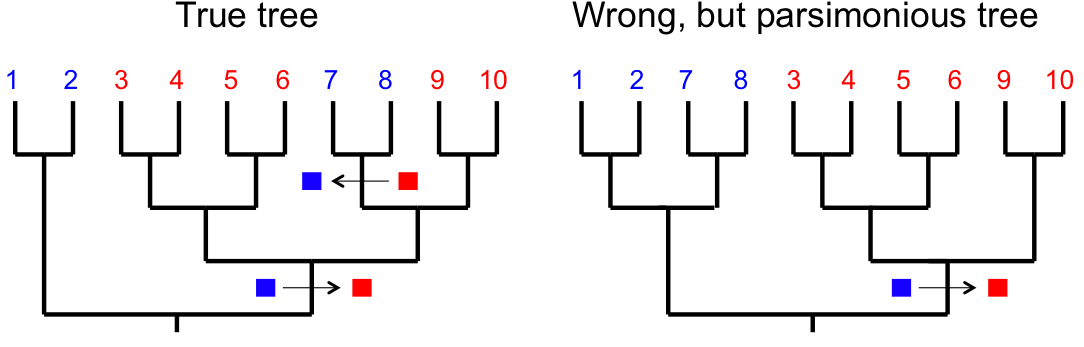
If a character reverts to an ancestral state, this can affect phylogenetic inference by creating false signals of relationship.

2. The Parsimony Principle

Maximum Parsimony

A method of phylogenetic inference that selects the tree(s) requiring the fewest evolutionary changes to explain the observed data.

Key concepts in parsimony analysis:

Key issue: How to separate homoplasy from homology (true shared ancestry)
Parsimony criterion: Favors hypotheses that maximize congruence and minimize homoplasy
Optimization problem: Find the tree with the minimum number of character state changes

Character Fit to Trees

The "fit" of a character to a tree is defined as the minimum number of steps (changes) required to explain the observed distribution of character states at the tips.

Different trees require different numbers of changes to explain the same character data

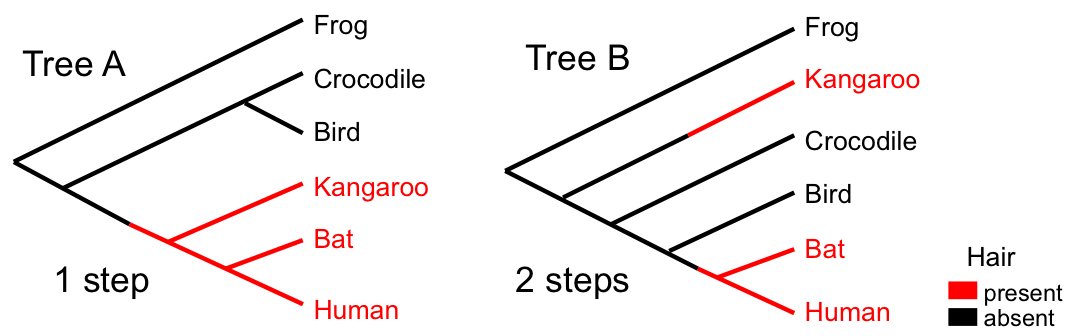
Parsimony Calculation

Given a set of characters (e.g., aligned sequences):

For each character, determine the minimum number of steps on a given tree
Sum over all characters to get the tree length
The most parsimonious trees (MPTs) have the minimum tree length

Parsimony Informative Sites

Not all characters contribute equally to distinguishing between alternative trees:

Parsimony-informative sites must have:

At least two different character states
Each state appearing in at least two taxa

Examples of non-informative sites:

Invariant sites: All taxa have the same state (always score 0)
Singleton sites: Only one taxon differs (always score 1)

Identifying Informative Sites

Site	Pattern	Informative?	Reason
1	AAAA	No	Invariant
2	AAAG	No	Singleton
3	AAGG	Yes	Two states, each in ≥2 taxa
4	AGTC	No	No state in ≥2 taxa

3. Computing Parsimony Scores

The Small Parsimony Problem

Given a tree topology and character data at the tips, find:

The minimum number of changes required for each character
The ancestral states that achieve this minimum

Dynamic Programming Solution

We can solve this efficiently using dynamic programming (Sankoff algorithm):

Sankoff Algorithm

For each node $v$ and each possible state $X$, calculate $m[v,X]$ = minimum cost of the subtree rooted at $v$ if $v$ has state $X$.

For leaf nodes:

m[v,X] = \begin{cases} 0 & \text{if character state for } v \text{ is } X\\ \infty & \text{otherwise} \end{cases}

For internal nodes (with children L and R):

m[v,X] = \min_Y\{m[L,Y] + c(X,Y)\} + \min_Z\{m[R,Z] + c(X,Z)\}

where $c(X,Y)$ is the cost of changing from state $X$ to state $Y$.

Computing parsimony length for a character

Dynamic programming computes optimal ancestral states bottom-up

Complexity Analysis

For the small parsimony problem:

Time complexity: $O(nS^2L)$
- $n$ = number of taxa (gives $2n-1$ nodes in rooted binary tree)
- $S$ = number of possible states (4 for DNA)
- $L$ = sequence length
- At each node: $O(S^2)$ calculations
Space complexity: $O(nS)$ to store the dynamic programming table

Fitch Parsimony

For the special case where all changes have equal cost (unweighted parsimony), Fitch (1971) developed a faster algorithm:

The Fitch algorithm uses set operations for unweighted parsimony

Fitch Algorithm

Phase 1 (Bottom-up):

For each leaf, assign its observed state
For each internal node with children having state sets $S_L$ and $S_R$:
- If $S_L \cap S_R \neq \emptyset$: assign $S_L \cap S_R$ (intersection)
- If $S_L \cap S_R = \emptyset$: assign $S_L \cup S_R$ (union) and count one change

Phase 2 (Top-down):

Assign specific ancestral states using the sets computed in Phase 1

Fitch Algorithm Example

Consider a simple tree with tips having states: ((A,G),(A,T))

Left child of root: A ∩ G = ∅, so assign {A,G}, cost = 1
Right child of root: A ∩ T = ∅, so assign {A,T}, cost = 1
Root: {A,G} ∩ {A,T} = {A}, so assign {A}, no additional cost
Total parsimony score = 2

4. Finding Optimal Trees

The "large parsimony problem" involves finding the tree topology (or topologies) with the minimum parsimony score:

Search Strategies

Exhaustive search: Evaluate all possible trees
- Guarantees finding all MPTs
- Only feasible for small numbers of taxa (≤10-12)
Branch-and-bound: Intelligent exhaustive search
- Uses lower bounds to eliminate parts of tree space
- Still guarantees finding all MPTs
- Practical for up to ~20-25 taxa
Heuristic search: Not guaranteed to find optimal trees
- Necessary for larger datasets
- Various strategies for exploring tree space

Branch-and-Bound Example

Branch-and-bound prunes search space by eliminating partial trees that cannot be optimal

Key insight: If a partial tree already has a parsimony score higher than a complete tree we've found, we can abandon that path.

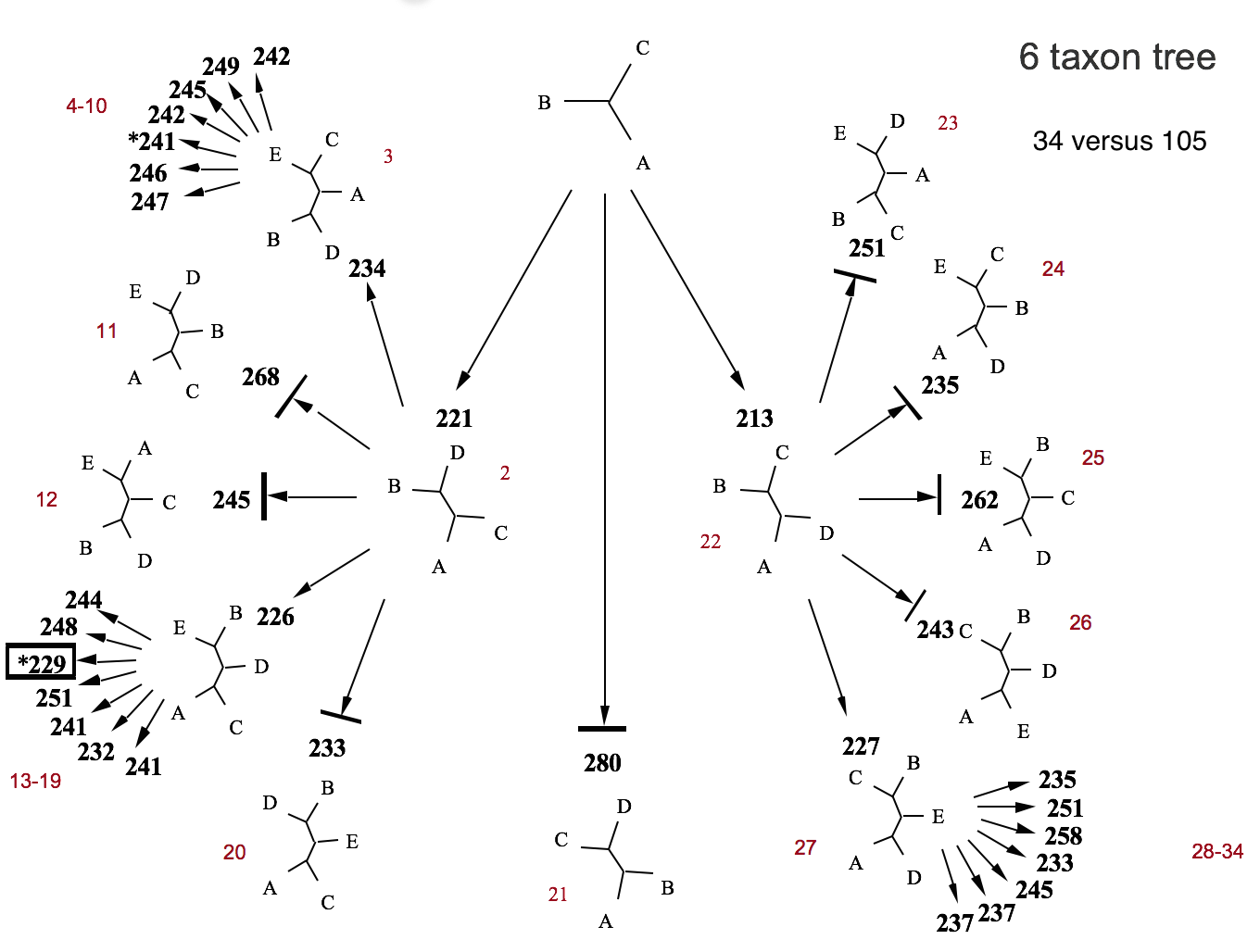
Heuristic Search Methods

Since the number of trees grows exponentially (NP-complete problem), heuristic methods are essential for larger datasets:

General Heuristic Strategy

Generate starting tree(s)
- Stepwise addition
- Star decomposition
- Random trees
Local search via branch swapping
- Nearest Neighbor Interchange (NNI)
- Subtree Pruning and Regrafting (SPR)
- Tree Bisection and Reconnection (TBR)

Branch Swapping Methods

NNI (Nearest Neighbor Interchange):
- Swaps adjacent branches
- Fastest but most limited
- Can get stuck in local optima
SPR (Subtree Pruning and Regrafting):
- Detaches a subtree and reattaches elsewhere
- More extensive search than NNI
TBR (Tree Bisection and Reconnection):
- Breaks tree into two subtrees and reconnects
- Most extensive rearrangements
- Best for escaping local optima

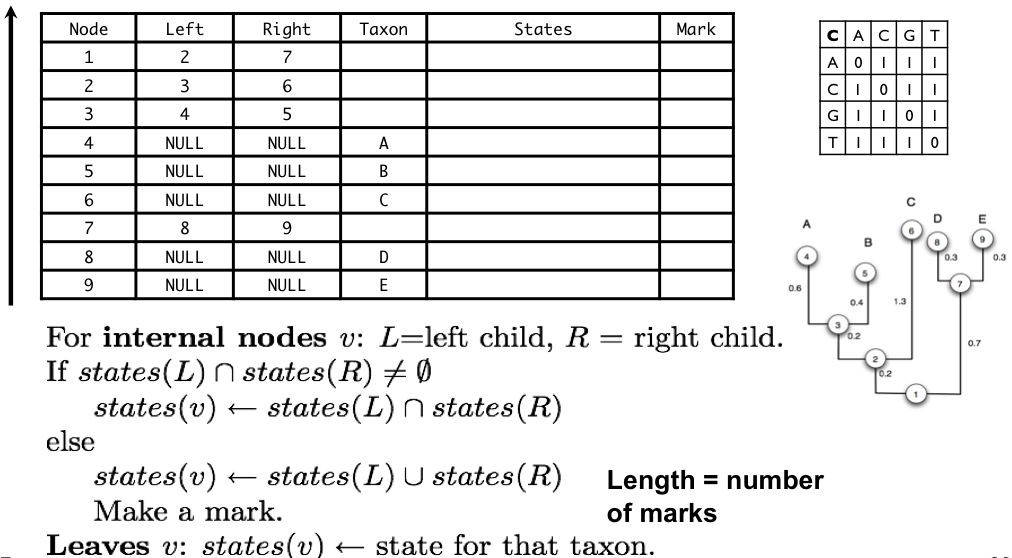
5. Tree Representation in Computers

Understanding how trees are stored in memory is crucial for implementing phylogenetic algorithms:

Trees can be represented as tables showing parent-child relationships

Tree Traversal Orders

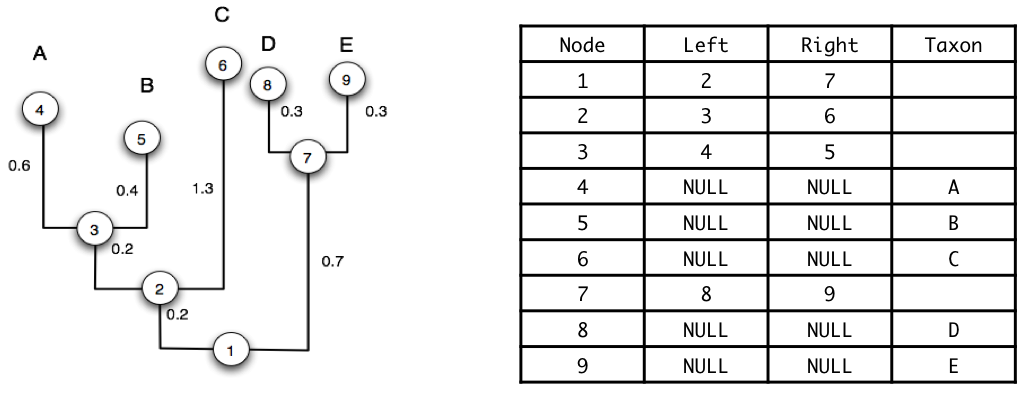
Pre-order: Visit parent before children (shown in table)
Post-order: Visit children before parent (used in Fitch algorithm)

Tree Traversal Example

For tree (((A,B),C),(D,E)) with nodes numbered as in the figure:

Pre-order: 1 → 2 → 3 → 4(A) → 5(B) → 6(C) → 7 → 8(D) → 9(E)
Post-order: 4(A) → 5(B) → 3 → 6(C) → 2 → 8(D) → 9(E) → 7 → 1

Note: The table in the figure shows nodes in pre-order, which is why they're numbered 1-9 in that sequence.

6. Parsimony Summary

Advantages of Parsimony

Simple, intuitive principle (Occam's Razor)
No explicit evolutionary model required
Fast algorithms for scoring trees
Can handle any type of character data
Identifies synapomorphies (shared derived characters)

Limitations of Parsimony

Can be inconsistent under certain conditions (long branch attraction)
Doesn't account for multiple substitutions on a branch
All changes treated equally (unless weighted)
No measure of uncertainty or support
No branch length estimation

Long Branch Attraction: Parsimony can incorrectly group long branches together because multiple changes on long branches can create false homoplasies.

Key Points to Remember

The small parsimony problem (scoring a tree) is efficiently solved by dynamic programming
The large parsimony problem (finding optimal trees) has no efficient solution
Maximum parsimony finds trees requiring the fewest evolutionary changes
Not based on an explicit evolutionary model
Best suited for datasets with low homoplasy

Software for Parsimony Analysis

PAUP*: Comprehensive phylogenetic analysis with excellent parsimony implementation
TNT: Optimized for large datasets, very fast
MEGA: User-friendly interface, good for teaching
MPBoot: Ultrafast bootstrap approximation for parsimony

Check Your Understanding

What makes a site parsimony-informative?
How does the Fitch algorithm differ from the general Sankoff algorithm?
Why is branch-and-bound better than exhaustive search?
What is the difference between the small and large parsimony problems?
Under what conditions might parsimony give misleading results?