Multiple Sequence Alignment

1. What is a Multiple Sequence Alignment?

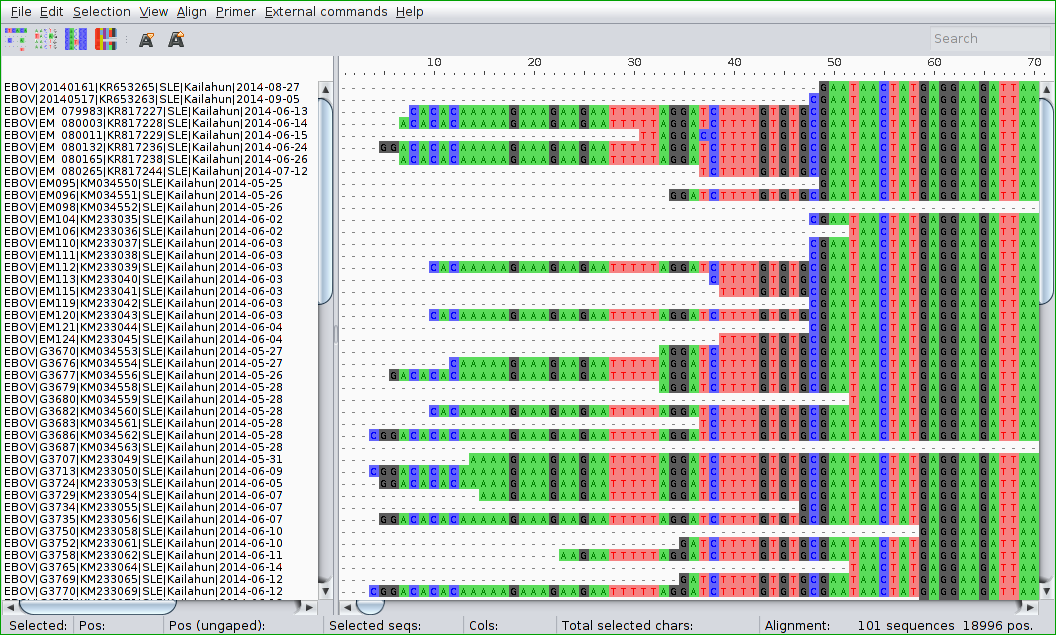
Multiple sequence alignment (MSA) is the process of aligning three or more biological sequences (protein or nucleic acid) to identify regions of similarity that may indicate functional, structural, or evolutionary relationships.

Example of a multiple sequence alignment of Ebola virus sequences

Notation

Throughout this lecture, we'll use the following notation:

Why Multiple Sequence Alignment?

Multiple sequence alignments are essential for:

• Identifying conserved regions across species
• Predicting protein structure and function
• Constructing phylogenetic trees
• Identifying functional motifs and domains
• Designing PCR primers
• Understanding evolutionary relationships

2. Scoring Multiple Sequence Alignments

Sum of Pairs (SP) Scoring

The most commonly used scoring function for MSAs is the sum of pairs method, which calculates the total score as the sum of all pairwise alignment scores.

Example

Consider the following alignment:

A-CTCAT
A-GTC-T
ACGTC-T

Let's calculate scores for specific columns:

• Column 3 score: We have C, G, G
  • $s(C,G) + s(C,G) + s(G,G) = \text{mismatch} + \text{mismatch} + \text{match}$
  • Total = $2 \times \text{mismatch score} + \text{match score}$
• Column 6 score: We have A, -, -
  • $s(A,-) + s(A,-) + s(-,-) = 2 \times \text{gap penalty} + s(-,-)$
  • Note: $s(-,-)$ is typically 0 (no penalty for aligning two gaps)

Problems with Sum of Pairs Scoring

Mathematically, the issue is that:

Tree-based Scoring

A more biologically motivated approach considers the evolutionary tree relating the sequences:

Comparison of sum of pairs scoring versus tree-based scoring

Tree-based scores are thought to be more biologically appropriate, but they have practical limitations:

• We don't know the true evolutionary tree
• We need to infer ancestral characters at internal nodes
• Different parts of the alignment may have different evolutionary histories (due to recombination)

Despite its theoretical limitations, sum of pairs scoring is almost always used in practice due to its computational simplicity.

3. Multidimensional Dynamic Programming

The Naïve Approach

We can extend the pairwise alignment dynamic programming approach to multiple sequences. Define $F(i_1,i_2,\ldots,i_N)$ as the score of the best alignment up to positions $i_1, i_2, \ldots, i_N$ in sequences $1, 2, \ldots, N$.

The recurrence relation becomes:

Visualization of the multidimensional dynamic programming matrix

Computational Complexity

The naïve dynamic programming approach has prohibitive computational requirements:

The MSA Algorithm

Carrillo & Lipman (1988) developed an improved algorithm that uses bounds on pairwise alignments to reduce the search space:

The MSA algorithm reduces the search space by constraining pairwise alignment scores

While this is a significant improvement, it's still impractical for most real-world alignment problems with more than a few sequences.

4. Progressive Alignment Methods

Given the computational limitations of exact algorithms, practical MSA methods use heuristic approaches. The most successful of these is progressive alignment.

General Strategy

Progressive alignment builds up the MSA by successively aligning sequences or groups

Key decisions in progressive alignment:

1. Order of alignments: Which sequences to align first?
2. Alignment strategy: Allow only sequence-to-group, or also group-to-group?
3. Scoring method: How to score alignments involving groups?

Guide Trees

Progressive alignment algorithms use "guide trees" to determine the order of alignment:

A guide tree determines the order in which sequences are progressively aligned

UPGMA Tree Construction

The Unweighted Pair Group Method with Arithmetic Mean (UPGMA) is commonly used to build guide trees:

The Feng-Doolittle Algorithm

Published in 1987, this was one of the first practical progressive alignment algorithms:

1. Calculate pairwise distances: Align all pairs of sequences and convert alignment scores to evolutionary distances:
   $$d(k,l) = -\log\frac{S(A^{(k)},A^{(l)})-S_{\text{rand}}}{S_{\text{max}}-S_{\text{rand}}}$$
2. Build guide tree: Use UPGMA or similar clustering algorithm
3. Progressive alignment: Starting from the leaves, align sequences following the guide tree

Sequence-to-Group Alignment

Aligning a sequence to an existing group alignment

Group-to-Group Alignment

Aligning two group alignments together

Progressive Misalignment

A major limitation of progressive alignment is that errors made early in the process cannot be corrected later:

Example of how early alignment decisions can lead to suboptimal final alignments

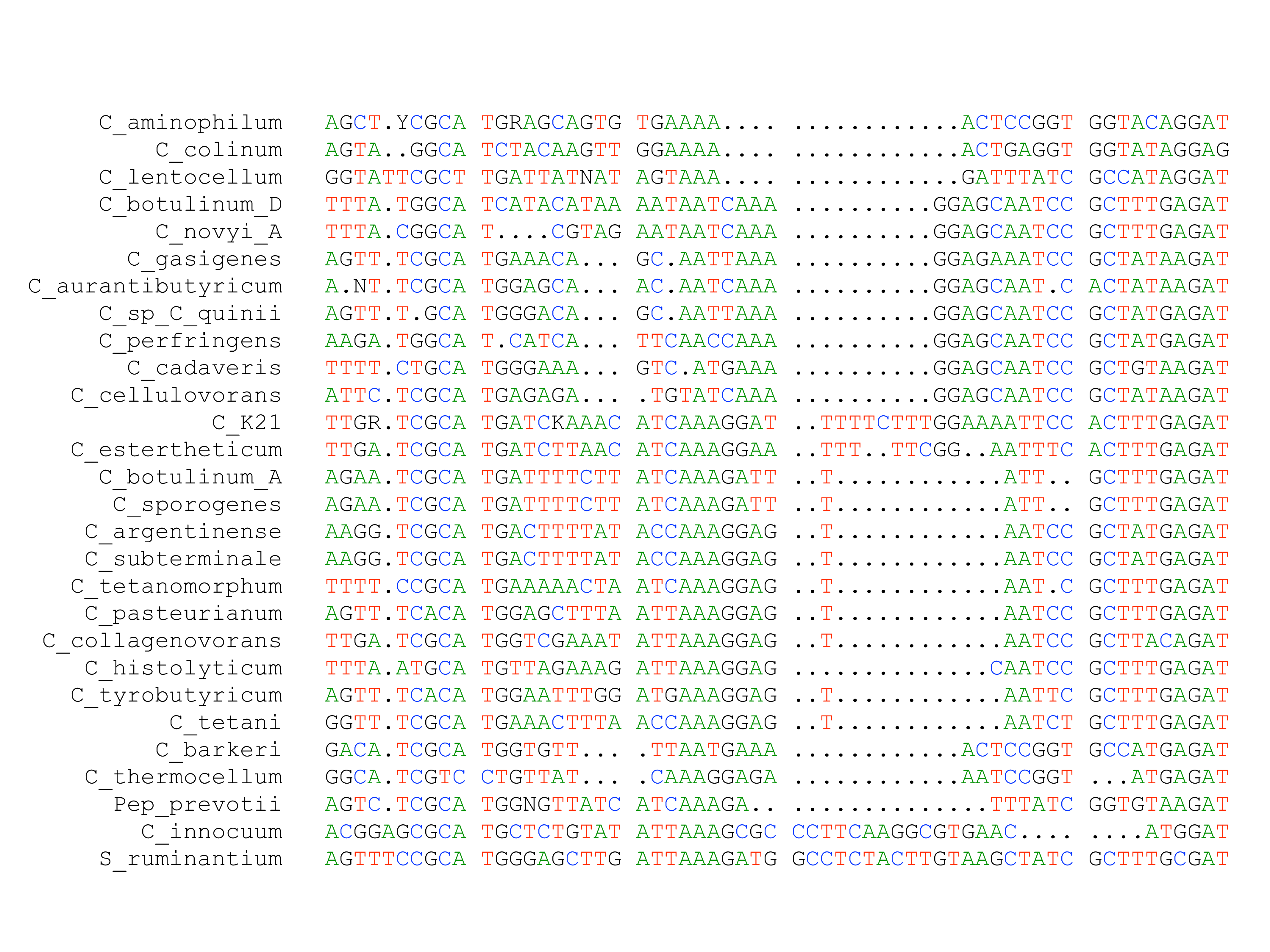
Profile Alignment

Modern progressive alignment methods use profile alignment to align groups of sequences:

Profile alignment considers the frequency of each character at each position

The total alignment score becomes: $S(A) + S(B) + S(A \times B)$

CLUSTALW

Thompson, Higgins, and Gibson (1994) developed CLUSTALW, which became one of the most widely used MSA programs (with over 55,000 citations!).

CLUSTALW is essentially the Feng-Doolittle algorithm with profile alignment and many additional heuristics:

1. Calculate all pairwise distances
2. Construct guide tree using UPGMA or neighbor-joining
3. Progressively align using sequence-sequence, sequence-profile, and profile-profile alignment

5. Iterative Refinement Methods

Iterative refinement methods attempt to improve an initial alignment by making small changes and accepting improvements (hill climbing to a local optimum).

The Barton-Sternberg Algorithm (1987)

1. Find the two most similar sequences and align them
2. Find the sequence most similar to the profile of the current alignment and add it
3. Repeat step 2 until all sequences are included
4. Refinement phase: Remove each sequence and realign it to the profile of the others
5. Repeat step 4 until convergence or a fixed number of iterations

Other Iterative Approaches

• Simulated annealing: Accept some score-decreasing moves to escape local optima
• Genetic algorithms: Maintain a population of alignments and evolve them
• Hidden Markov Models: Use probabilistic models for alignment

6. Practical Considerations and Limitations

General Limitations

Statistical Approaches: Fitting vs. Modeling

There are two philosophical approaches to sequence alignment:

BAli-Phy: A Bayesian Approach

Suchard and Redelings (2006) developed BAli-Phy, which jointly estimates alignment and phylogeny using Bayesian inference:

BAli-Phy provides uncertainty estimates for both alignment and phylogeny

This approach is philosophically optimal but computationally intensive, limiting its use to smaller datasets.

Summary

1. Scoring: Multiple sequence alignments are typically scored using sum of pairs, despite theoretical limitations
2. Exact algorithms: Dynamic programming can find optimal alignments but scales as $O(n^N)$, making it impractical for most problems
3. Progressive alignment: Practical heuristic that builds alignments incrementally using a guide tree
4. Iterative refinement: Can improve initial alignments but may still converge to local optima
5. Trade-offs: Current methods balance biological accuracy with computational feasibility
6. Future directions: Bayesian approaches offer principled solutions but need computational improvements